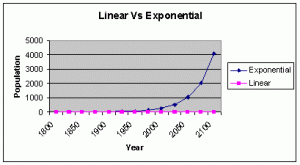
Linear vs Exponential Growth:

Linear growth and Exponential growths are different. Linear growth go in a patter while Exponential growths don’t. On an expression linear growth will be Y=3x+4. Exponential growth in an expression will be Y=1.04^x*5,000. On a graph a linear growth goes at a constant rate while on the other hand exponential growth may go at a constant rate but then will just stop and go in a line.

Scientific Notation:

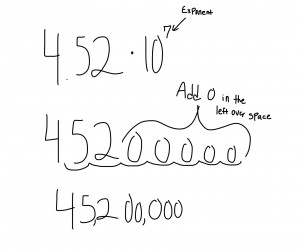
A scientific notation is something that looks like 3.25*10^5. The different between 10^5 and 3.25*10^5 is that 10^5 is 10*10*10*10*10 while 3.25*10^5 is 325,000. The exponential tell you the amount of times you will move after the decimal. 10^5  is only showing that you will multiply ten five times.

Simplifying Exponent Expressions Using The Product and Quotient Rules:

Simplifying Exponents are easy once you get the hang of it. An example of it is (-9)^4, this would be simplified too (-9)(-9)(-9)(-9) which equals too 6561. The 5 different Exponent Properties I learned are; The Power Rule, The Quotient Rule, The Distributive Rule for Quotients, The Product Rule, and The Distributive Rule for Products.

The Power Rule: The Power Rule’s general rule is that when a power is raised to a power, we multiplu the exponents, and the base stays the same. An example of this would be (B^30)^4 equals B^120. Its B^120 because you would multiply the power numbers.

The Quotient Rule: The general rule for this one is when you divide two exponential exponents with the same base, subtract the exponents and keep the same base. An example would be 12^5/12^4 which turns into 12^5-4 which equals too 12^1.

The Distributive Rule for Quotients: The rule for this one is when you divide two exponential expressions inside the parenthesis, and its raised to the power, we distribute it to both the numerator and the denominator. An example is (10/b)^5 equals 10^5/b^5.

The Product Rule: The rule for this one is when you multiply two exponential expressions with the same base, add the exponents and the base always stays the same. This is an example 17^10*17^21 converts too 17^10+21 equals too 17^31.

The Distributive Rule for Products: The last one we learned also had a rule, its rule was that when youvhave two or more terms raised to the same power, the power will be distributed to the terms. One example of this is (6*7*1)^10 equals 6^10*7^10*1^10.

Negative Exponents:

With negative exponents you you have a negative exponential number, for example 4.75*10^-3. This however does not make the number negative. It only shows that the decimal will be moved to the negative side (the left)  instead of the positive side (the right).