Blog 25: AAS Congruence and ASA Congruence
When you are trying to find out if two triangles are congruent, you don’t need to find all of the side lengths and angles. A faster way to find out is to only use the least amount of information that you need to determine if they are congruent. The least amount of information that you need are two pairs of congruent corresponding angles and one pair of corresponding sides. There are two different versions of this, ASA and AAS. ASA means that the corresponding side is between the two corresponding angles. AAS means that the corresponding side isn’t between the two corresponding angles.
Blog 26: Using Flowcharts
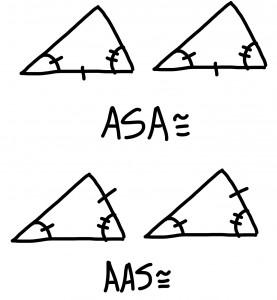
When you are determining whether two triangles are congruent, you need to show all the steps you took to make that decision. One method to do this is flowcharts. In a flowchart, you start by stating all of the information that was given. From there, you have to find out if any corresponding sides or angles are congruent by using any properties. Finally, you have to write that they are congruent and state the condition underneath it.
Blog 27: Triangle Congruence Conditions
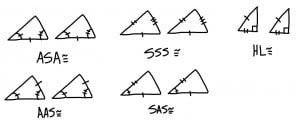
Two triangles are only congruent if they fall under one of the five triangle congruence conditions. These five conditions are ASA, AAS, SSS, SAS, and HL. I described ASA and AAS earlier in this blog. ASA is when there are two congruent corresponding angles and one pair of corresponding sides in between. AAS is when there are two congruent corresponding angles and one pair of corresponding sides that isn’t between the two angles. SSS is when all corresponding sides of the triangle are equal. SAS is when there are two pairs of corresponding sides and a pair pf corresponding angles in between. HL is when there is a right triangle and you know that the hypotenuses are equal and one pair of corresponding sides are congruent.
Blog 28: Determining a Midpoint
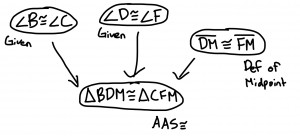
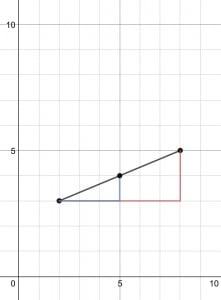
The midpoint is the exact middle of a line segment. Normally, when you determine a midpoint, you find the length of the line segment and divide it by two. However, on a graph, it is a little bit different. Say you have a line segment with the points at (2,3) and (8,5). First, you have to make a slope triangle, so it would go 6 to the right and up 2. To find the midpoint, you have to find half of the slope triangle. So that would be 3 to the right and up 1. That means that the midpoint is (5,4).
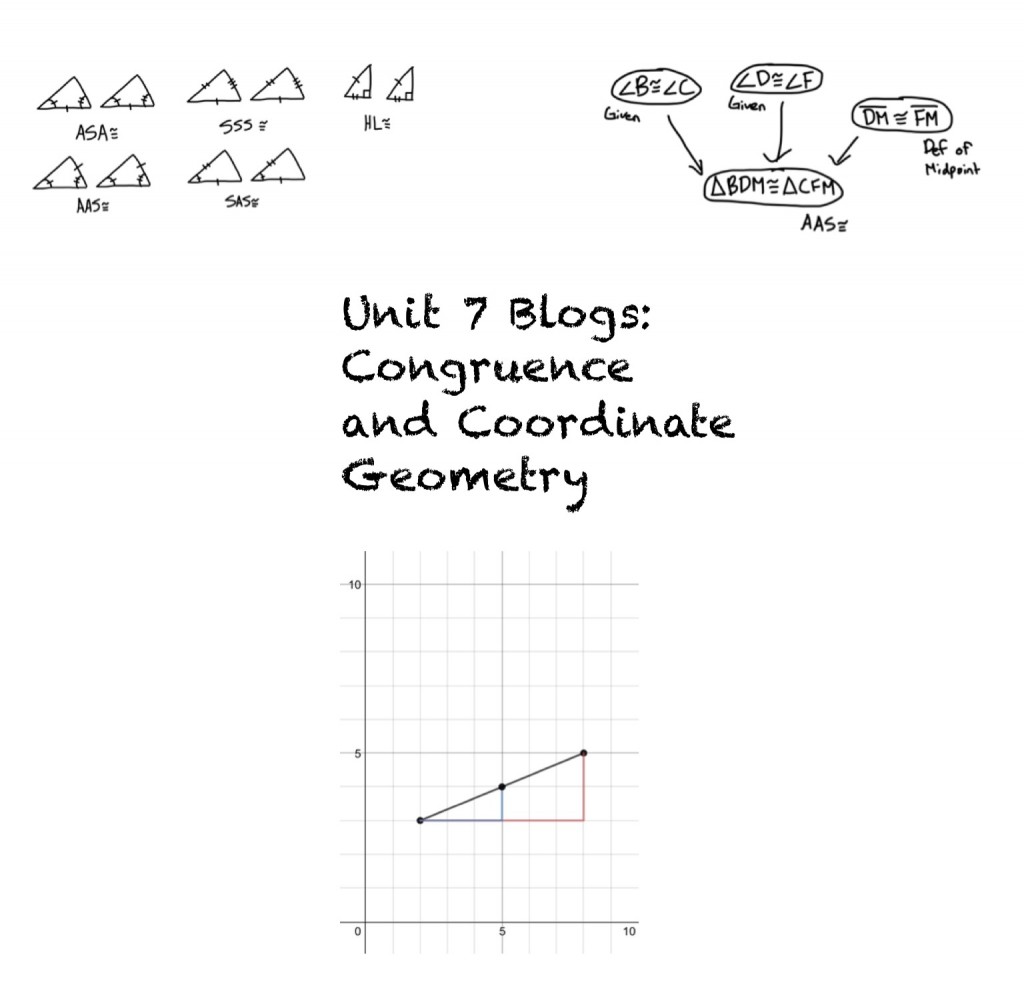



Leave a Reply