Investigating y = b^x   5/1

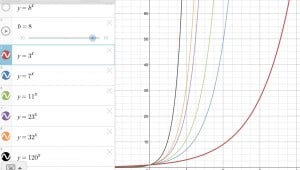
During class today we did lesson 8.1.1 where we had to experiment with the equation y = b^x. I found out that the variable b controls the slope and increase of the equation. While doing this I observed the difference between the b when it was changed. For example, if b was 120 and in another equation b was 3, 120 grows at a faster rate.

During this lesson I learned how the b effects the graphs growth depending on the b’s number. The smaller the number the slower it accelerates. I learned that any equation in the y = b^x, will never equal zero.

Multiple Representations Web for Exponential Functions 5/1

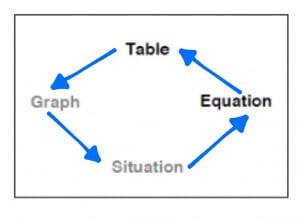
In lesson 8 we learned about exponential functions. After learning about exponential functions I can create an equation, table, graph, and situation based on the information that was given. The class and I learned different methods to figure out missing information to fill in the table and graph.

I believe that I still need to practice making situations for exponential functions, so I can get used to writing them. The more practice I get at all these skills, the easier math will be for me.

Updated Web for Exponential Functions 5/3

In lesson 8.1.3 I used tables, graphs, and equations. The lesson asked to make a simple and compound graph to show which interest grows at a faster rate. The tables helped create the graph points. I also learned how to make a step function on a graph. I had to create equations off the situations. After making the graph I could see that compounded interest grows at a faster rate giving you more money the longer its in a bank.

Graph → Equation for Exponential Functions 5/8

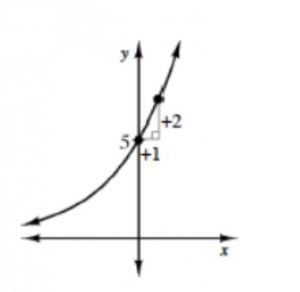
There are different methods to write an exponential equation given a graph that includes the y-intercept. The first step I took to write an equation is to find the y-intercept for the equation y=a*b^x. A in this equation represents the y-intercept and b is the slope. The second step is to find the slope and this graph already has the slope, so its easier to figure it out. I have noticed that for exponential slopes they are usually a decimal. I also noticed that the graph is curved when its exponential. For this graph it looks like the slope is 2 but its really 1.4. You would write this in an equation like, y=5*1.4^x.

Important Ideas about Exponential Functions 5/10

The last blog for math in my eighth grade year is about what I learned in this chapter. For example, I learned about exponential graphs, tables, and how to write an exponential equation. I learned that exponential decay is when its exponential but the numbers are decreasing. Exponential equations are one of the main ideas of chapter 8. This is important to learn because exponential is related to compound and simple interest which is used in car loans and banks when dealing with money. This will help me in the future when I need to go to a bank.